数组中的逆序对(Leetcode 剑指Offer51)

发表于 | 分类于 ， ， | | 本文总阅读数 次
| 字数统计: 1.5k | 阅读时长 ≈ 6
Leetcode 剑指Offer51

1

题目分析

   这个题目还有一种另外的表达方式，交换两个相邻数，使得数组有序的最少交换次数，两个题目的意思是相同的，都是寻找逆序数的对数。这个题目最早是2020年写的题解，后面随着学习的深入，掌握了一些更高级的数据结构，可以有另外的思路求解本题，对这篇博客进行补充。

暴力法

这个题目最简单的方法是暴力，遍历每一个位置，并且对于每一个位置枚举在它之前的所有元素，记录比它大的元素的个数即可。时间复杂度为$O(n^2)$，空间复杂度为$O(1)$。

1
2
3
4
5
6
7
8
class Solution(object):
    def reversePairs(self, nums):
        res = 0
        for i in range(1, len(nums)):
            for j in range(i):
                if nums[j] > nums[i]:
                    res += 1
        return res

分治算法

暴力法当然可以求解，但是时间复杂度太高。我们考虑一种情况，两个有序数组，进行合并时，是否可以利用一些大小关系缩小时间复杂度。
这里使用官方题解中的数据进行演示，小伙伴们也可以去观看官方题解中的视频教程进行学习。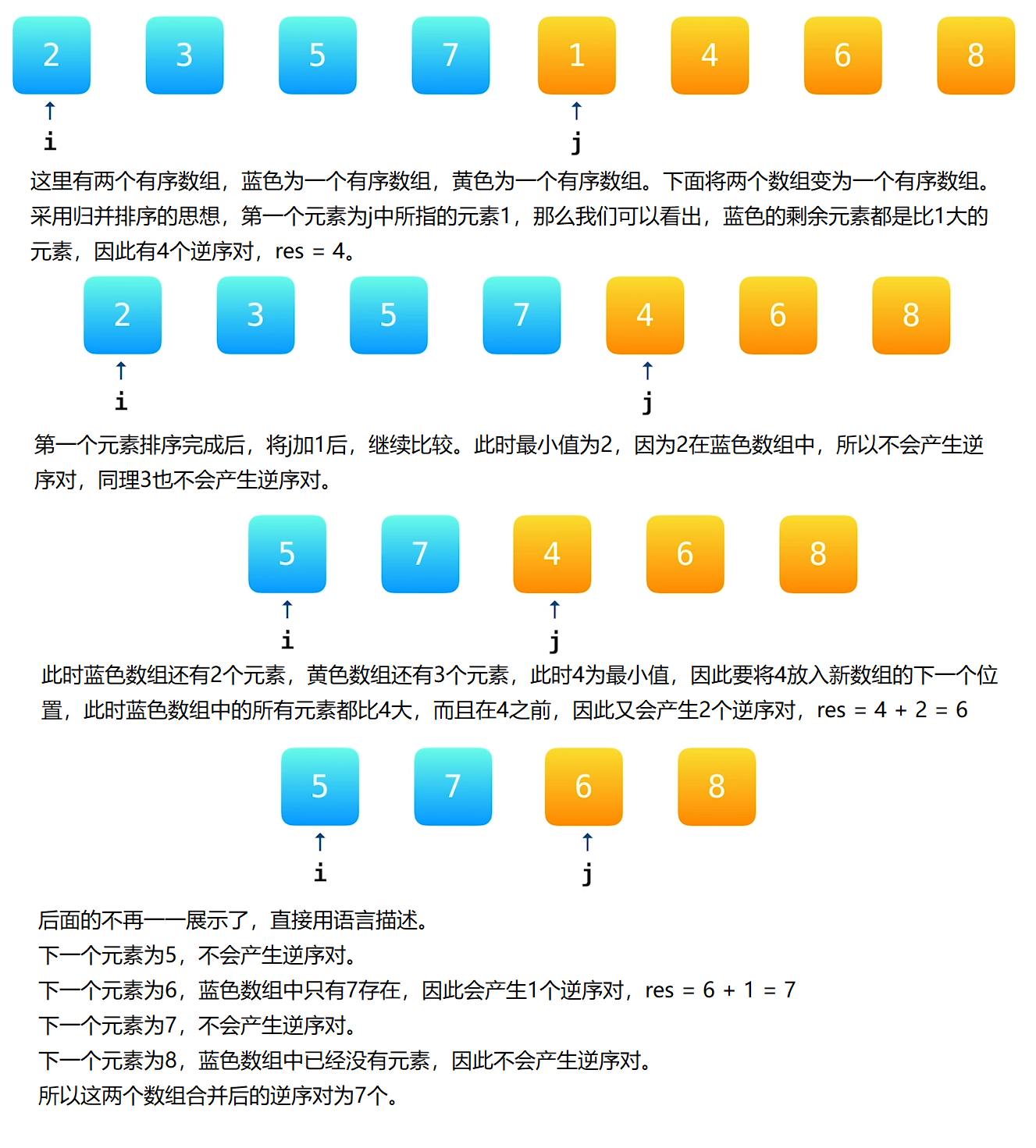
1
由两个有序数组合并为一个有序数组的过程就是一个归并排序的过程。先将长度为n的数组，逐步分解，直到长度为1，然后进行合并，在合并的过程中求解逆序对的个数。
时间复杂度为$O(nlog(n))$，空间复杂度为$O(n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution(object):
    def reversePairs(self, nums):
        def merge(nums, begin, mid, end):
            if begin == end:
                return 0
            new_nums = []
            res = 0
            left, right = begin, mid + 1
            while left < mid + 1 and right < end + 1:
                if nums[left] <= nums[right]:
                    new_nums.append(nums[left])
                    left += 1
                else:
                    new_nums.append(nums[right])
                    right += 1
                    res += mid - left + 1
            new_nums += nums[left:mid + 1] + nums[right:end + 1]
            nums[begin:end + 1] = new_nums
            return res

        def partition(nums, begin, end):
            if begin < end:
                return partition(nums, begin, (begin + end) // 2) + partition(nums, (begin + end) // 2 + 1, end) + merge(nums, begin, (begin + end) // 2, end)
            else:
                return 0

        return partition(nums, 0, len(nums) - 1)

在新的题解中，我们使用java语言进行重写归并算法。思路和上面的题解大致相同，但是实现有一些差异。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
class Solution {
    public int reversePairs(int[] nums) {
        return merge(nums, 0, nums.length - 1);
    }

    private int merge(int[] nums, int left, int right) {
        if (left >= right) {
            return 0;
        }
        int mid = (left + right) >> 1;
        int leftPtr = left;
        int rightPtr = mid + 1;
        int leftCnt = merge(nums, left, mid);
        int rightCnt = merge(nums, mid + 1, right);
        int cnt = leftCnt + rightCnt;
        while (leftPtr <= mid) {
            while (rightPtr <= right && nums[leftPtr] > nums[rightPtr]) {
                rightPtr++;
            }
            cnt += rightPtr - mid - 1;
            leftPtr++;
        }
        
        int[] tmpNums = new int[right - left + 1];
        int idx = 0;
        leftPtr = left;
        rightPtr = mid + 1;
        while (leftPtr <= mid && rightPtr <= right) {
            tmpNums[idx++] = nums[leftPtr] < nums[rightPtr] ? nums[leftPtr++] : nums[rightPtr++]; 
        }
        while (leftPtr <= mid) {
            tmpNums[idx++] = nums[leftPtr++];
        }
        while (rightPtr <= right) {
            tmpNums[idx++] = nums[rightPtr++];
        }
        for (int i = 0; i < tmpNums.length; i++) {
            nums[left + i] = tmpNums[i];
        }
        return cnt;
    }
}

树状数组

本题是寻找逆序对，逆序对就是找某个数前面有多少数大于它。是不是可以转换一下思路，逆序对等于寻找某个数前面有多少数小于它。

从后向前遍历，将元素放到对应的位置上，类似于计数排序，计算某个数x后面有多少数字小于它的时候，就是统计从最小值到x - 1对应计数之和。

根据这个思路，就非常接近于前缀和的题目，每次插入元素，等于在该位置+1，查找时，需要查找从nums[min]到nums[x - 1]的元素之和。

因为这个题目等价于修改元素的前缀和，因此可以通过树状数组的方法将其时间复杂度优化到O(log(n))

在树状数组中，元素的索引都是大于等于0的，但是本题存在负数，且元素的值可能很大。在逆序对中，我们不需要关心数字的绝对大小，仅需要保证数字的相对大小即可，所以[7, 5, 6, 4]逆序对的数量等价于[4, 2, 3, 1]，如果将元素从1开始，那么就需要对数据映射。

本题我们不仅仅要学会如何使用树状数组和求解逆序对，也需要掌握元素的映射方法。可以先添加到set集合中，因为集合是去重的，设集合中的元素有x个，说明元素可以从1映射到x。再将元素进行排序，从小到大对应到相应的索引。例题排序为[4, 5, 6, 7]，4对应索引0 + 1，5对应索引1 + 1，就可以将原数组进行压缩。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
class Solution {
    HashMap<Integer, Integer> reflect;

    int[] tree;

    public int reversePairs(int[] nums) {
        getReflect(nums);
        int res = 0;
        for (int i = nums.length - 1; i >= 0; i--) {
            int reflectVal = reflect.getOrDefault(nums[i], 0);
            res += query(reflectVal - 1);
            add(reflectVal);
        }
        return res;
    }

    private void getReflect(int[] nums) {
        Set<Integer> set = new HashSet(nums.length);
        for (int x : nums) {
            set.add(x);
        }
        int[] tmp = new int[set.size()];
        int idx = 0;
        for (int x : set) {
            tmp[idx++] = x;
        }
        Arrays.sort(tmp);
        reflect = new HashMap<>(tmp.length);
        for (int i = 0; i < tmp.length; i++) {
            reflect.put(tmp[i], i + 1);
        }
        tree = new int[tmp.length + 1];
    }

    private void add (int x) {
        for (; x < tree.length; x += lowBit(x)) {
            tree[x]++;
        }
    }

    private int query(int x) {
        int cnt = 0;
        for (; x > 0; x -= lowBit(x)) {
            cnt += tree[x];
        }
        return cnt;
    }

    private int lowBit(int x) {
        return x & -x;
    }
}

刷题总结

  这个题目算一个非常有难度的题目，是笔试面试中的高频考点。归并排序已经不是笔试面试中的考点了，因为比较简单，所以通过考察归并排序的变形题，考察小伙伴们的思维能力和代码能力，这非常重要。而树状数组的解法作为小伙伴们提高的解法，如果觉得归并排序可以轻松写出来，可以尝试挑战。

-------------本文结束感谢您的阅读-------------
0%